布尔运算
本章主要介绍了如何基于上一章构建的逻辑门电路构建出 ALU(Arithmetic Logic Unit/算术逻辑单元)
ALU 是核心的单元,它执行所有的算术和逻辑操作。因此,要理解中央处理器(Central Processing Unit, CPU)以及整个计算机的工作方式,构建 ALU 功能 模块是很重要的一步。

基础知识
二进制数
计算机是基于二进制系统的,用于两个 n 位数字二进制加法的计算机硬件可以由三位(两个计算位加上一个进位)加法的逻辑门构建而成。
有符号二进制数
n 位二进制系统可以产生2的n次方个不同的组合。如果必须用二进制码表示有符号数,有个简单的方法就是,将这个空间分成两个相同的子集,一个子集用来表示正数,另一个表示负数。从理想的角度来说,编码规则应该按照如下原则来进行:有符号数的引入应该使硬件实现的复杂程度尽可能小。
有符号数的二进制表示促进了很多编码体系的发展。如今几乎所有计算机都采用称为 2-补码(2's complement)的编码方式,也称为基补码(radix complement)。在n位的二进 制系统中,数x的补码定义如下:
if (x != 0){
return 2^n-x
} else {
return 0
}
这种表示法有个特别有吸引力的特征:任何两个用补码表示的有符号数的加法和与正数的加法完全相同。
简单来说,我们发现补码表示法可以实现任何两个有符号数的加法而不需要特殊的硬件。那么减法是怎样的呢?前面说过,在补码表示里面,对有符号数x的取反,也就是计算 -x,要将 x 的所有位取反然后再加 1。因此,减法可以被看成 x一y = x +(一y)。这样,硬件的复杂度也保持在最小。
这些理论结果的实际含义是很重要的。基本上,它们意味着能用单一芯片(称为算术逻辑单元,ALU 即 Arithmetic Logical Unit)将硬件执行的所有基本算术操作和逻辑操作都封装起来。
规范详述
加法器
我们介绍三个加法器,并由此引出多位加法器芯片: - 半加器(Half-adder):用来进行两位加法。 - 全加器(Full-adder):用来进行三位加法。 - 加法器(Adder):用来进行两个n位加法。
我们也介绍了一种特殊的加法器,称为增量器(incrementer),用来对指定的数字加1。
- 半加器:进行二进制数加法的第一步就是要能够对两个二进制位进行相加。我们把结果的LSB(Least Significant Bits 最右边的一位) 位称为sum,MSB(Most Significant Bits 最左边的一位) 位称为 carry。图
- 全加器:现在已经知道了如何对两个位进行相加,全加器就是支持进位运算的半加器,用来对三个位相加。跟半加器一样,全加器电路也会产生两个输出:加法的LSB位和进位。
- 加法器:存储器和寄存器电路用n-位的形式来表示整数,n可以是16、32、64等等。进行n-位加法的芯片称为多位加法器(multi-bit adder),或者简称为加法器。
- 增量器:专门构建一个“对指定数字加1”的电路,这样做会带来很多便利。
算术逻辑单元(ALU)
接下来就是构建 Hack 计算的 ALU 模块了
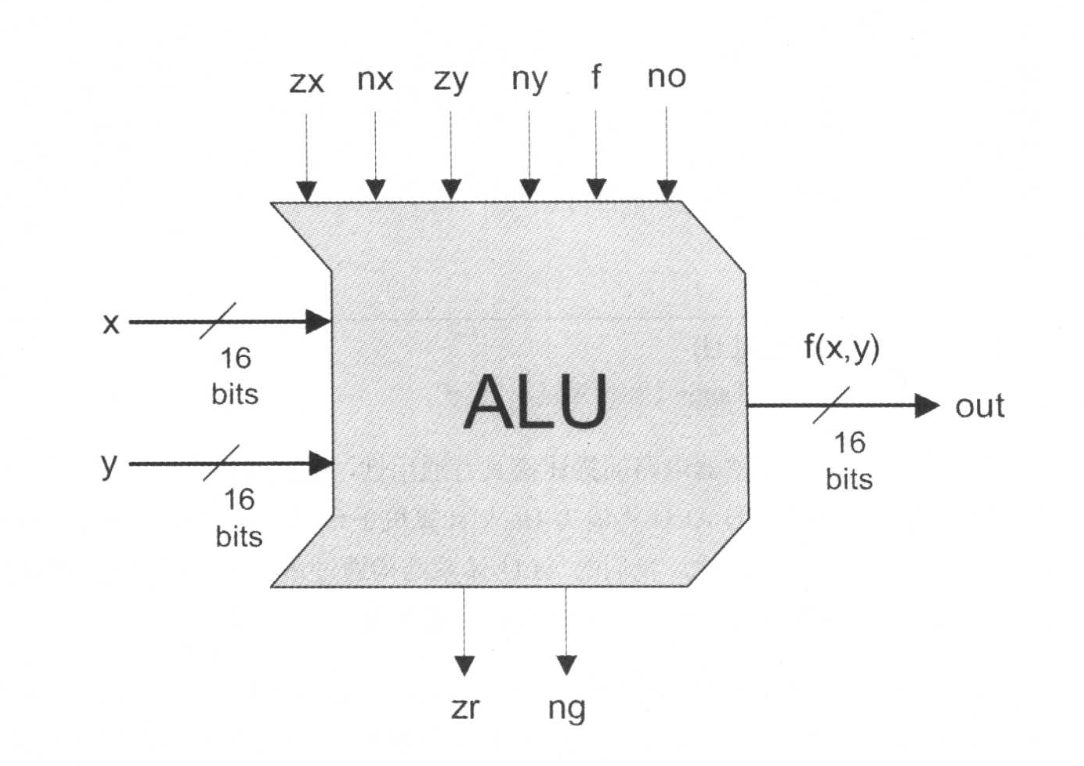
Hack 的ALU 计算一组固定的函数out=f(x,y),这里x和y是芯片的两个 16-位输入,out是芯片的16-位输出,f是位于一个函数表中的函数,该函数表由18个固定函数组成。
我们通过设置六个称为控制位(control bits)的输入位来告诉 ALU 用哪一个函数来进行何种函数计算。下图给出了用伪代码表示的详细的输入/输出规范。
要注意的是,这6个控制位的每一位指示ALU 来执行某个基本操作。这些操作的各种组合可以让 ALU 计算多种有用的函数。因为全部操作都是由6个控制位引起的,那么 ALU 可以对 2^6=64个不同的函数进行操作。下图列出了这些函数中的18种。
可以看到,我们是通过将6个控制位设置成函数f(x,y)所对应的编码,来指示 ALU 计算该函数。从这点来看,下面描述的ALU 内部逻辑应该产生如图中列出的f(x,y)的 输出值。当然,这不是碰巧产生的,而是精心设计的结果!

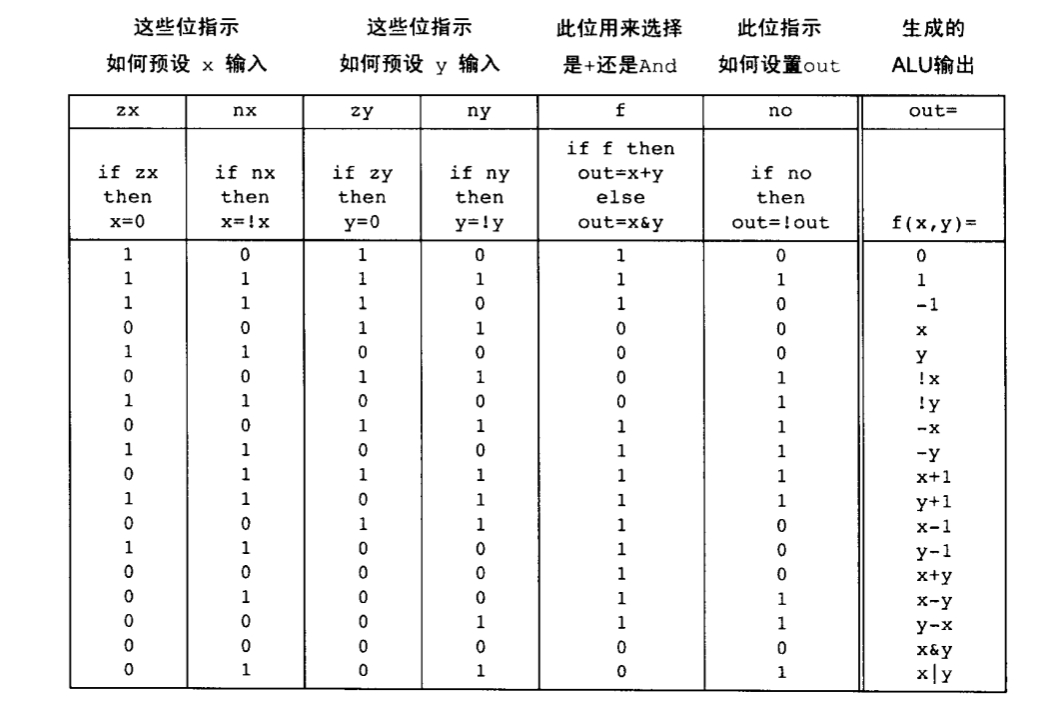
对这个特殊ALU 的设计过程的描述是很有启发意义的。首先,我们制作了一张函数列表,其中包含了所有我们希望计算机能够执行的原始函数。接着,应用倒推法得出如何 在二进制模式下操作x,y来实现期望的操作。这些处理要求以及“使ALU 逻辑尽可能简单”的目标,导致我们的在设计中使用6个控制位,每一位都直接对应一个简单的二进制 操作。这样的 ALU 构造简单且结构良好。从硬件的角度来说,简单的、良好的结构意味着便宜但功能强大的计算机系统。
项目
HalfAdder
CHIP HalfAdder {
IN a, b; // 1-bit inputs
OUT sum, // Right bit of a + b
carry; // Left bit of a + b
PARTS:
Xor(a = a, b = b, out = sum);
And(a = a, b = b, out = carry);
}
FullAdder
CHIP FullAdder {
IN a, b, c; // 1-bit inputs
OUT sum, // Right bit of a + b + c
carry; // Left bit of a + b + c
PARTS:
HalfAdder(a = a, b = b, sum = s1, carry = c1);
HalfAdder(a = s1, b = c, sum = sum, carry = c2);
Xor(a = c1, b = c2, out = carry);
}
Add16
CHIP Add16 {
IN a[16], b[16];
OUT out[16];
PARTS:
HalfAdder(a = a[0], b = b[0], sum = out[0], carry = c0);
FullAdder(a = a[1], b = b[1], c = c0, sum = out[1], carry = c1);
FullAdder(a = a[2], b = b[2], c = c1, sum = out[2], carry = c2);
FullAdder(a = a[3], b = b[3], c = c2, sum = out[3], carry = c3);
FullAdder(a = a[4], b = b[4], c = c3, sum = out[4], carry = c4);
FullAdder(a = a[5], b = b[5], c = c4, sum = out[5], carry = c5);
FullAdder(a = a[6], b = b[6], c = c5, sum = out[6], carry = c6);
FullAdder(a = a[7], b = b[7], c = c6, sum = out[7], carry = c7);
FullAdder(a = a[8], b = b[8], c = c7, sum = out[8], carry = c8);
FullAdder(a = a[9], b = b[9], c = c8, sum = out[9], carry = c9);
FullAdder(a = a[10], b = b[10], c = c9, sum = out[10], carry = c10);
FullAdder(a = a[11], b = b[11], c = c10, sum = out[11], carry = c11);
FullAdder(a = a[12], b = b[12], c = c11, sum = out[12], carry = c12);
FullAdder(a = a[13], b = b[13], c = c12, sum = out[13], carry = c13);
FullAdder(a = a[14], b = b[14], c = c13, sum = out[14], carry = c14);
FullAdder(a = a[15], b = b[15], c = c14, sum = out[15], carry = c15);
}
Inc16
CHIP Inc16 {
IN in[16];
OUT out[16];
PARTS:
Add16(a = in, b[0] = true, b[1..15] = false, out = out);
}
AUL
/**
* ALU (Arithmetic Logic Unit):
* Computes out = one of the following functions:
* 0, 1, -1,
* x, y, !x, !y, -x, -y,
* x + 1, y + 1, x - 1, y - 1,
* x + y, x - y, y - x,
* x & y, x | y
* on the 16-bit inputs x, y,
* according to the input bits zx, nx, zy, ny, f, no.
* In addition, computes the two output bits:
* if (out == 0) zr = 1, else zr = 0
* if (out < 0) ng = 1, else ng = 0
*/
// Implementation: Manipulates the x and y inputs
// and operates on the resulting values, as follows:
// if (zx == 1) sets x = 0 // 16-bit constant
// if (nx == 1) sets x = !x // bitwise not
// if (zy == 1) sets y = 0 // 16-bit constant
// if (ny == 1) sets y = !y // bitwise not
// if (f == 1) sets out = x + y // integer 2's complement addition
// if (f == 0) sets out = x & y // bitwise and
// if (no == 1) sets out = !out // bitwise not
CHIP ALU {
IN
x[16], y[16], // 16-bit inputs
zx, // zero the x input?
nx, // negate the x input?
zy, // zero the y input?
ny, // negate the y input?
f, // compute (out = x + y) or (out = x & y)?
no; // negate the out output?
OUT
out[16], // 16-bit output
zr, // if (out == 0) equals 1, else 0
ng; // if (out < 0) equals 1, else 0
PARTS:
// zx
Mux16(a = x, b = false, sel = zx, out = x1);
// nx
Not16(in = x1, out = x2);
Mux16(a = x1, b = x2, sel = nx, out = x3);
// zy
Mux16(a = y, b = false, sel = zy, out = y1);
// ny
Not16(in = y1, out = y2);
Mux16(a = y1, b = y2, sel = ny, out = y3);
// f
And16(a = x3, b = y3, out = f1);
Add16(a = x3, b = y3, out = f2);
Mux16(a = f1, b = f2, sel = f, out = o1);
// no
Not16(in = o1, out = o2);
Mux16(a = o1, b = o2,sel = no, out=out, out[0..7]=outlow, out[8..15]=outhigh, out[15]=ng);
// zr outno = 0时,zr = 1
Or8Way(in = outlow,out = outor8waylow);
Or8Way(in = outhigh,out = outor8wayhigh);
Or(a = outor8waylow,b = outor8wayhigh, out = nzr);
Not(in = nzr,out = zr);
}